Модели коллективного страхования крупных рисков

,

где индексы соответствуют исходам "успех с первой попытки", "успех со второй попытки" и "неудача". Это достигается выполнением требования:

.

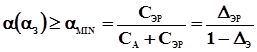Область допустимых решений W

ПЗС

, следовательно, будет выше минимального уровня страховой ставки aMIN

.

Для второго активного субъекта – П введенное выше условие выполняется автоматически. Расчет минимально допустимой надежности PMIN

может быть выполнен на множестве допустимых решений. С учетом сделанных предположений для данной модели максимальные потери могут составлять:

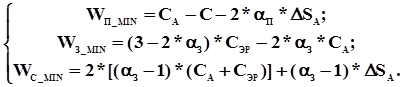
Максимальные возможные доходы участников выражаются величинами:

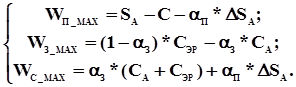
Модель 4.3

. Повторная реализация вообще не предусматривается (в силу возможной уникальности условий и срока его проведения). В этом случае придем к следующей модели.

П страхует свои затраты, сделанные им при оплате реализации. Как и прежде предполагается, что первоначальные выплаты равны:

C

– S

Э

.

Именно возможность возврата этой суммы получает П при заключении договора страхования. При успешном выполнении проекта расходы П равны C

, т. к. он выплачивает еще и прибыль S

Ээксплуатирующей организации. В случае неудачи потерю затрат компенсирует С. Таким образом, ожидаемые средние доходы П составят:

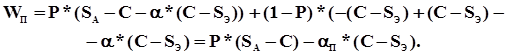
Для З, соответственно:

.

Так как эксплуатирующая организация застраховала свою прибыль, то эта прибыль меньше, чем максимально возможная (S

Э

), но в то же время она гарантированно больше нуля, чему она равнялась бы при неуспешном выполнении проекта и отсутствии договора страхования.

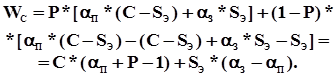
Т.о. модель 4.3 задается уравнениями:

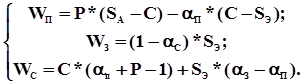
Рассмотрение минимальных экономических требований участников операции страхования одиночной реализации проекта позволяет выделить области допустимых решений для каждого из них при назначении страховых ставок. При этом для З риск невелик и ограничение на величину a

З

тривиально – a

З

< 1

. Следовательно, область допустимых решений будет фактически определяться требованиями со стороны П и С, т.е. W

ПЗС

=

W

ПС

, и выражаться результатом решения системы неравенств:

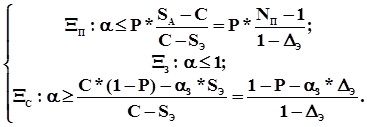
При условии принятия договорного уровня a

З

с использованием дополнительной информации, которой располагают договаривающиеся стороны, граничное значение вероятности успешной реализации будет определяться выражением:

, .

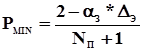Так, например, для случая относительно низкорентабельного проекта (N

П

= 1,2

) при a

З

= 0,1

и D

Э

= 0,2

искомая величина вероятности составит 0,9

, что является весьма жестким требованием к З и П, учитывая необходимость наличия некоторого запаса по надежности для возможных уступок на переговорах с С. Повышая N

П

до уровня 1,5

, можно снизить нижний предел вероятности до значения PMIN

= 0,8

.

Модель 5

. Модель этого типа соответствует случаю создания взаимного страхового фонда (ВСФ) П и З. Наличие такого фонда оправдано при проведении серии проектов.

Предполагается, что ВСФ образуется при отсутствии предложения на рынке страховых услуг по компенсации потерь при реализации проекта и используется в целях распределения нагрузки между его учредителями. Страховые компании привлекаются только для компенсации потерь ожидаемой прибыли.