Модели коллективного страхования крупных рисков

,

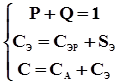где C

– номинальная стоимость реализации проекта.

Содержательное описание моделей коллективного страхования космических программ

Модель 1.

Первый граф (см. рис. 12) характеризует ситуацию взаимного страхования потребителя и владельца средств СЭ и в данном исследовании не рассматривается как модель с двумя участниками страхования.

Модель 2.

Данная модель предполагает наличие страховых отношений только между владельцем объекта страхования (первичным потребителем ожидаемого выходного эффекта, П) и страховщиком, С.

Так как в модели отсутствует непосредственное отношение ЗС, то при заключении договора страхования между П и С одним из пунктов может быть передача права страховщику вести судебное преследование владельца СЭв случае ненадлежащей реализации проекта, приведшей к возникновению страхового случая. Это преследование будет завершено в пользу страховщика с вероятностью Q

Э

и страховое покрытие (или его часть) будет взыскано с организации занимающейся реализацией проекта.

Предполагается, что П страхует только свои прямые расходы C

, которые он затрачивает реализацию проекта, причем выплата прибыли З (S

Э

) производится авансом перед проведением работ и при возникновении страхового случая может быть взыскана в пользу страховщика в составе стоимости C

.

С учетом этих предположений модель страхования задается уравнениями ожидаемых доходов субъектов страхования.

При наличии договора страхования между П и С с нетто-ставкой a

П

и страхуемой суммой (C

) ожидаемые доходы субъектов П, З и С находятся как математические ожидания по распределению вероятностей возможных исходов запуска КА.

При благоприятном исходе П получает доход:

или

;

равный ожидаемым доходам от реализации проекта (S

А

) за вычетом расходов на реализацию проекта (C

) и страховой премии (a

П

*C

). Предполагается, что размер ожидаемых доходов S

А

составляет величину, достаточную для покрытия издержек на обеспечение реализации проекта.

При неблагоприятном исходе S

А

= 0

, расходы на подготовку возмещаются страховщиком и доход равен:

.

Вероятность первого события равна P

, второго – (1 –

P

)

и тогда:

W

П

= P

* [SA

– C

* (1 +

a

П

)] + (1 – P

) * (-

a

П

* С) =

= P * SA – (

a

П + P) * C .

Ожидаемый доход З находится с учетом сделанного предположения о предварительной оплате владельцем объекта страхования стоимости затрат C

ЭР

и прибыли S

Э

, а также возможности регрессного иска со стороны страховой компании при неблагоприятном исходе по вине З.

При неблагоприятном исходе реализации проекта, т.к. величина a

П

* C

уже оплачена страховщику, величина иска может составлять (1-

a

П

) * C

, т.е. при наступлении страхового случая по вине З его доход равен:

C

Э

– (1 –

a

П

) * C

.

В случае же наступления страхового случая, приведшего к потере объекта страхования при отсутствии эксплуатационной ошибки:

C

Э

.

При благоприятном исходе доход З равен СЭ

. Вероятности событий в указанных случаях составляют: первого события Q

Э

, второго – (

Q

– Q

Э

)

и третьего – P

. Ожидаемый доход З в результате подготовки будет равен: